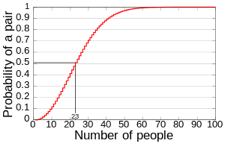
The birthday paradox is strange, counter-intuitive, and completely true. It’s only a “paradox” because our brains can’t handle the compounding power of exponents. We expect probabilities to be linear and only consider the scenarios we’re involved in.
When in a room with 22 other people, if a person compares his or her birthday with the birthdays of the other people it would make for only 22 comparisons—only 22 chances for people to share the same birthday. But when all 23 birthdays are compared against each other, it makes for much more than 22 comparisons.
With 23 people we have 253 pairs: 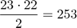
The chance of 2 people having different birthdays or in other words the chance of a unique pair: 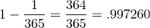 . The chance of 253 unique pairs:
. The chance of 253 unique pairs: 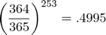
The birthday paradox proven with Belgian open data
Statistics Belgium recently published the birth statistics of the past seven years so I verified the birthday paradox against the births in Belgium.
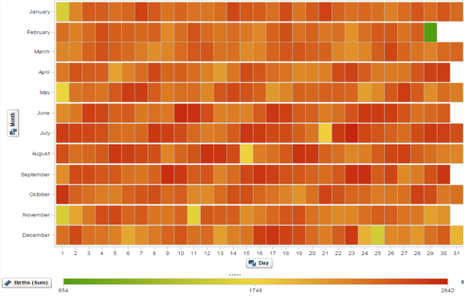
The numbers taught me that deliveries were not evenly distributed over all days. On average 347 babies are born every day in Belgium (between January 1st 2008 and December 31st 2014) but on the graphs below we clearly see that the maternity hospital was not consistently crowded every day of the year.
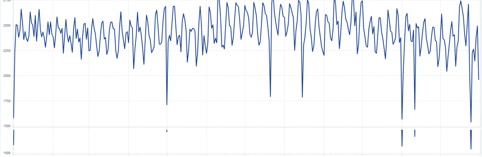
July 23rd, June 10th and September 9th were the busiest days at the Belgian maternity hospitals the past seven years. In general we observe more births in summer.
The day with the lowest total number of newborns is February 29th, which obviously makes sense. One place higher in the ranking and thus also quite unpopular as birthday are December 25th, preceded by five other bank holidays (January 1st, November 11th, May 1st, August 15th and July 21st ). Looks like Belgian women don’t like to give birth on their day off!
The birthday paradox proven amongst the SAS BeLux employees
I already hear you think that the birthday paradox is not proven on these rather large amounts of data, so I went to the HR department of my company and asked for the birthdays of all employees. There are 22 different days on which at least two employees celebrate their birthday.
However, since there are 143 people working at SAS Institute Belux, the birthday paradox is still not proven. So I took six random samples of 23 employees each, and guess what: in 50% of the cases I found a shared birthday! I also took a sample of 75 random employees and immediately 6 pairs of birthdays matched.
So next time you’re with another 20 to 30 persons in the room, ask everyone for their birthday and find out if the birthday paradox works!